Bon, je l’admets, le titre est un peu violent, surtout si c’est ma femme qui le lit. N’empêche…

Egal au rapport entre la circonférence d’un cercle et son diamètre, π est pour beaucoup de mathophobes le symbole de l’oppression de leur enfance par les hordes sévères et sauvages des éducateurs à collier de barbe ou chignon qui ne juraient que par Euclide, Pythagore et Thalés. Je connais une personne raisonnablement éduquée pour qui cette pauvre lettre grecque est quasiment la svastika de la dictature mathématicienne sur notre civilisation…

Pour moi, π est une source de fascination et de poésie sans fond, l’incarnation de la beauté des nombres et de leur danse infinie et complexe qui soutient chaque facette de l’univers. Des tas de livres lui ont été – et lui seront encore – consacrés, des hommes ont passé des jours, des mois, des années à la poursuite de la connaissance de ses arcanes, et malgré la simplicité de sa définition, les mathématiciens lui découvrent encore maintenant de nouvelles propriétés.

Je ne vais pas vous abreuver d’indigestes formules dans ce texte. Mon but est de vous raconter quelques histoires autour de π, dans l’espoir d’entrebâiller pour vous la porte vers les mondes où j’aime à me promener maintenant que les maths sont pour moi un plaisir, et plus un enjeu.

Dura lex, sed lex

A tous ceux qui pensent que le gouvernement ne peut pas tout, l’état américain de l’Indiana a failli opposer un démenti cinglant (et bien cinglé).

En 1897, un certain Edwin J. Goodwin a soumis aux représentants de l’Indiana une proposition de loi accordant au susdit état la possibilité d’utiliser et d’enseigner sans le moindre frais la méthode révolutionnaire de quadrature du cercle qu’il avait développée peu de temps auparavant. Jusque là, rien d’absurde au premier abord…

Rédigée en des termes dépassant les compétences en mathématiques des législateurs, le texte fut baladé de commission en commission à la manière d’une patate chaude, et était sur le point d’être voté quand le Professeur C. A. Waldo de l’Université de Purdue qui passait là pour une toute autre affaire fut interpellé par un membre de l’assemblée sur le texte de Goodwin. Waldo manqua avaler son lorgnon, et permit d’éviter que l’état d’Indiana devienne le premier à fixer par la Loi la valeur (erronée) de la plus célèbre constante mathématique.

Voyez-vous, si l’expression “quadrature du cercle” ne vous est pas inconnue, c’est qu’il s’agit du plus célèbres des trois problèmes impossibles – les deux autres étant la trisection de l’angle et le doublement du cube – qui ont occupé les mathématiciens sérieux depuis l’Antiquité jusqu’à la preuve de leur impossibilité, et les mathématiciens loufoques à partir de là.

En termes simples, la quadrature du cercle est l’hypothétique méthode permettant de construire uniquement à l’aide d’un compas et d’une règle non graduée un carré ayant la même surface qu’un cercle donné. Ferdinand von Lindemann avait démontré en 1882 le caractère impossible (et soupçonné de longue date) de cette méthode, mais il semble que sa démonstration avait laissé Goodwin de marbre.

La démonstration de Goodwin se basait tout bonnement sur une redéfinition de π en lui attribuant la valeur de 3,2 bien plus pratique à manipuler que l’encombrant 3,14159265358979… Après tout, pourquoi pas ? (Parce que !) Sur sa lancée, Goodwin attribua aussi à la racine de 2 la valeur 10/7, après quoi il fonça sans doute vers la fumerie d’opium la plus proche pour chercher de nouvelles constantes mathématiques à violer sauvagement par tous les trous…

Sans l’intervention inopinée de Waldo, l’Indiana aurait donc fixé par la loi la valeur de π, ce qui aurait sans doute provoqué la destruction instantanée de l’univers dans un immense éclat de rire. Bien fait pour Dieu, il n’avait qu’à faire plus simple !

π appreciation day

La Femme a sa journée internationale (le 8 mars), les Droits de l’Enfant aussi (le 20 novembre), et plus important encore, le Fromage a le 27 mars. En fait, tout le monde et toute chose a sa journée, ce qui n’est pas un mince exploit vu qu’on ne dispose que de 365 jours… Toujours plus malin que les autres, π n’a pas un mais deux jours qui lui sont consacrés !

Le 14 mars (en anglais 3/14) a été reconnu officiellement “Pi Day” par la Chambre des représentants des USA. Chaque année à cette date, des zozos dans mon genre se réunissent pour manger des gâteaux (en anglais, π se prononce comme pie), réciter des décimales et d’une manière générale discuter de leur passion pour ce nombre unique.

L’autre jour de l’année, c’est le 22 juillet, le “Pi Approximation Day”, ainsi nommé car la fraction ²²⁄₇ (3,142857…) approxime π à moins d’1% près.

Ah, j’oubliais : lors du “Pi Day”, à l’université de Princeton, se déroule un concours de sosies d’Albert Einstein. Pourquoi ça ? Eh bien, tout simplement parce qu’Einstein, qui a vécu et travaillé là-bas une vingtaine d’années, est né un 14 mars.

 π vs. τ

On parle beaucoup de l’Irak, de l’Afghanistan, du Mali et des autres conflits qui pullulent depuis la nuit des temps sur notre bonne vieille Terre. Mais, ignorée de tous, boycottée des médias, une bataille fratricide fait rage sur Internet. N’écoutant que mon courage, j’ai enfilé ma panoplie de reporter de guerre, bravant tous les dangers pour vous informer…

A ma droite, le favori : π (Pi), 3000 ans de suprématie incontestée sur le monde des mathématiques, avec un cri de ralliement universel : “C = 2πr !”.

A ma gauche, le challenger : τ (Tau), porté depuis 2010 par le physicien Michael Hartl sur le ring de cette lutte fratricide (en effet, les deux nombres sont frères, puisque τ=2xπ).

La démarche de Hartl se base sur les nombreuses formules mathématiques comportant le facteur 2π, formules qui seraient simplifiées en le remplaçant par τ. ” The Tau manifesto “, la profession de foi de Hartl, est une charge enflammée contre la suprématie de π qui rallie chaque jour de plus en plus de partisans prêts à en découdre (sur les forums, rassurez vous) avec les horribles réactionnaires et leur contre-offensive (The Pi Manifesto). Jusqu’alors il n’y a pas eu de morts, mais avec ces zozos, tout est possible…

Et π c’est tout !

π est un nombre réel, irrationnel et transcendant. Tout à fait moi.

Certains pensent que π serait aussi un nombre normal, comme semble l’indiquer tout un faisceau d’indices relevés sur son expansion décimale (la suite des chiffres après la virgule) jusqu’à la 6 milliardième (!) décimale.

Qu’est ce qu’un nombre normal ? Tout simplement que dans l’infinité de chiffres après la virgule de π, les 10 chiffres de 0 à 9 se trouvent en proportion identique.

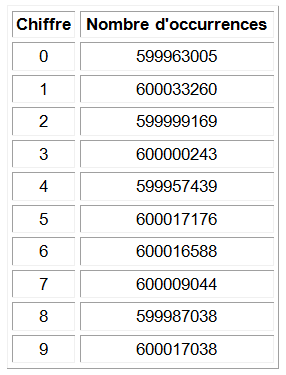
Bon. Et alors, me direz vous ? Eh alors, si π est normal, alors il est tout à fait possible qu’il s’agisse… roulements de tambours… d’un nombre UNIVERS !!!

Ah… Un nombre univers… Vous m’en direz tant. C’est quoi cette bête ?

π possède une infinité de chiffres après la virgule, ça, c’est prouvé. Et on a aussi prouvé que ces chiffres ne présentent aucune séquence qui se répète (comme dans 1/7 = 0,14285714285714285714…).  Parmi cette infinité, on retrouve bien évidemment les dix chiffres de 0 à 9. Il n’est guère besoin d’imagination pour concevoir que les 100 doublets de chiffres, de “00” à “99” se retrouvent aussi. Pour les 1000 triplets, de “000” à “999”, en cherchant bien, ça doit pouvoir se faire ; après tout, on parle d’une infinité de chiffres…

Eh bien, si π est un nombre univers, alors on peut poursuivre le raisonnement ci-dessus aussi loin qu’on le désire, ad libitum et ad infinitum. Ce qui signifie que quelque part, dans les profondeurs insondables de cette petite lettre grecque, on peut trouver toute suite de chiffres imaginable, de quelque longueur que ce soit. Votre numéro de téléphone, le mien (tiens, ça me fait penser que vous n’appelez pas souvent…), celui de ma mère (tiens, ça me fait penser que je n’appelle pas souvent…), celui de Laetitia Casta (où ça, où ça ?!?), les dates de naissance de chaque personne de votre entourage…

Si vous remplacez chaque lettre de l’alphabet par son rang (A=01, B=02… Z=26), chaque mot, chaque phrase, chaque livre écrit ou à écrire, tout ce qu’on peut représenter par des chiffres se trouve caché dans le rapport entre la circonférence d’un cercle et son diamètre. Ce qui inclut évidemment tout l’Internet, qui n’est après tout qu’un gros tas de 0 et de 1.

Evidemment, il ne suffit pas de savoir qu’une série de nombres est présente pour pouvoir la retrouver. Mais ça n’enlève rien à la poésie de la chose, n’est-ce pas ?